
ЖЭТФ, Том 117,
Вып. 4,
стр. 659 (Апрель 2000)
(Английский перевод - JETP,
Vol. 90, No 4,
p. 571,
April 2000
доступен on-line на www.springer.com
)
СТРУКТУРА ВЫСШИХ ПОПРАВОК К АСИМПТОТИКЕ ЛИПАТОВА
Суслов И.М.
Поступила в редакцию: 1 Ноября 1999
PACS: 74.50.+r; 74.60.Ge; 74.25.Fy; 74.72.Hs
Высокие порядки теории возмущений могут вычисляться методом Липатова, согласно которому они определяются перевальными конфигурациями - инстантонами - соответствующих функциональных интегралов. Для большинства теорий поля асимптотика Липатова имеет функциональную форму c aN Γ(N+b) (N - порядок теории возмущений), а относительные поправки к ней имеют вид ряда по степеням 1/N. Показано, что этот ряд факториально расходится, а его далекие коэффициенты могут быть вычислены в рамках процедуры, аналогичной липатовской: K-й коэффициент разложения имеет вид 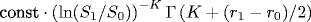 , где S0 и S1 - значения действия для первого и второго инстантонов рассматриваемой теории поля, а r0 и r1 - соответствующее им число нулевых мод; инстантоны удовлетворяют тому же уравнению, что и в методе Липатова, и предполагаются перенумерованными в порядке возрастания соответствующего им действия. Этот результат имеет универсальный характер и справедлив в любой теории поля, для которой асимптотика Липатова имеет указанный выше вид. , где S0 и S1 - значения действия для первого и второго инстантонов рассматриваемой теории поля, а r0 и r1 - соответствующее им число нулевых мод; инстантоны удовлетворяют тому же уравнению, что и в методе Липатова, и предполагаются перенумерованными в порядке возрастания соответствующего им действия. Этот результат имеет универсальный характер и справедлив в любой теории поля, для которой асимптотика Липатова имеет указанный выше вид.
|
|