
ЖЭТФ, Том 167,
Вып. 5,
стр. 611 (Май 2025)
(Английский перевод - JETP,
Vol. 140, No 5,
May 2025
доступен on-line на www.springer.com
)
Формализм безмодельного решения задачи рассеяния в системе трех частиц с кулоновским взаимодействием. Надпороговые осцилляции сечений рассеяния и реакций в системе 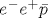
Градусов В.А., Яковлев С.Л.
Поступила в редакцию: 21 Октября 2024
DOI: 10.31857/S0044451025050013
Представлен безмодельный формализм для решения задачи рассеяния в системе трех частиц с кулоновским взаимодействием для энергий ниже порога развала системы на три частицы на основе уравнений Фаддеева-Меркурьева. Для решения задачи рассеяния используются асимптотические граничные условия, которые наряду с кулоновским взаимодействием между мишенью и спектатором в явном виде учитывают дальнодействующее дипольное взаимодействие, ответственное за аномальное надпороговое поведение сечений рассеяния и реакций (осцилляции Гайлитиса-Дамбурга). На основе эффективного численного метода прямого решения граничной задачи для уравнений Фаддеева-Меркурьева получены высокоточные сечения рассеяния антипротона на позитронии и сечения образования антиводорода в системе 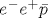 для ненулевых значений полного орбитального момента системы, подтверждающие наличие аномального порогового поведения сечений. для ненулевых значений полного орбитального момента системы, подтверждающие наличие аномального порогового поведения сечений.
|
|