
ЖЭТФ, Том 152,
Вып. 1,
стр. 147 (Июль 2017)
(Английский перевод - JETP,
Vol. 125, No 1,
p. 123,
July 2017
доступен on-line на www.springer.com
)
«Мягкие» моды спектра возбуждений, построенные на возмущениях решетки Абрикосова с одним квантом потока в элементарной ячейке
Овчинников Ю.Н.
Поступила в редакцию: 21 Февраля 2017
DOI: 10.7868/S0044451017070136
Исследуется спектр бесщелевых возбуждений, возникающих при возмущении решетки Абрикосова с одним квантом потока в элементарной ячейке. Особенный интерес представляют сверхпроводники со значением параметра Гинзбурга-Ландау κ , близким к единице. Найден спектр бесщелевых возбуждений, близких к нулевым сдвиговым модам, при произвольном значении угла φ между векторами элементарной ячейки. Исследование спектра возбуждений треугольной и квадратной решеток с одним квантом потока в элементарной ячейке показало, что по крайней мере в области значений параметра κ , близких к единице (κ > 1), существуют решения с большим единицы числом квантов потока, дающие меньшие значения свободной энергии по сравнению со значениями свободной энергии для треугольной решетки с одним квантом потока. При малых значениях импульса 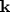 (в (в 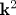 -приближении) спектр возбуждений «поперечной» моды в треугольной решетке не зависит от направления импульса, лежащего в плоскости, перпендикулярной магнитному полю. Для квадратной решетки (φ = π /2) поперечная мода анизотропна и в -приближении) спектр возбуждений «поперечной» моды в треугольной решетке не зависит от направления импульса, лежащего в плоскости, перпендикулярной магнитному полю. Для квадратной решетки (φ = π /2) поперечная мода анизотропна и в 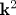 -приближении. -приближении.
|
|