Критическое поведение трехкомпонентной модели Поттса с вмороженным беспорядком на квадратной решетке
Бабаев А.Б., Муртазаев А.К.

Поступила в редакцию: 7 Марта 2025

DOI: 10.31857/S0044451025090081

PDF (436.7K)

Методом Монте-Карло исследовано критическое поведение трехкомпонентной модели Поттса с вмороженным беспорядком на квадратной решетке при концентрациях спинов p=1.00, 0.95, 0.90, 0.80. Рассмотрены системы с линейными размерами 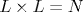, L=10-320. Для определения критической температуры использовался метод кумулянтов Биндера четвертого порядка. С применением теории конечно-размерного скейлинга определены критические индексы теплоемкости α , намагниченности β , восприимчивости γ и критический индекс радиуса корреляции u в рассмотренном интервале разбавлений p. Показано, что класс универсальности слабо разбавленной трехкомпонентной модели Поттса на квадратной решетке описывается новым набором критических индексов и этот набор отличается от соответствующего для чистой модели Поттса (p=1.00).